Calculus – II | Undergraduate Mathematics Notes
Vectors play a crucial role in describing physical quantities such as force, velocity, electric and magnetic fields. Vector calculus deals with the differentiation and integration of vector fields in space.
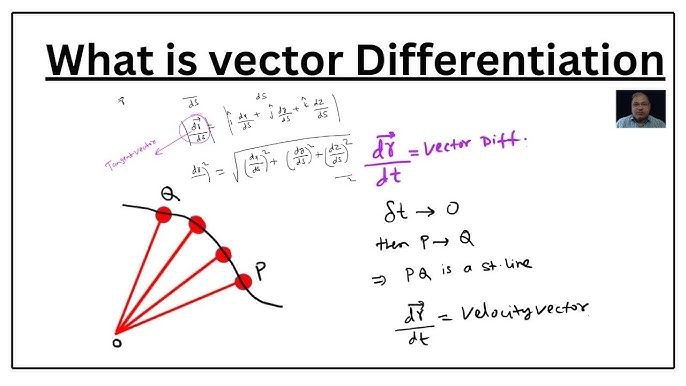
🔹 1️⃣ Vector Differentiation
Directional Derivative
Measures the rate of change of a scalar field in a given direction.
If f(x,y,z) is a scalar field and a^ is a unit vector:Da^f=∇f⋅a^
If this direction is normal to a surface, it is called the normal derivative.
Gradient of a Scalar Field
Gradient gives the maximum rate of change of a scalar field.∇f=(∂x∂f)i^+(∂y∂f)j^+(∂z∂f)k^
📌 Geometrical Interpretation
- Gradient is perpendicular to the level surface f=constant
- Its magnitude gives the steepest slope
Divergence of a Vector Field
Indicates how much a vector field is spreading out from a point.
For vector field A=Axi^+Ayj^+Azk^:∇⋅A=∂x∂Ax+∂y∂Ay+∂z∂Az
Curl of a Vector Field
Measures rotation in the field.∇×A=i^∂xAxj^∂yAyk^∂zAz
Del Operator (∇)
A differential operator:∇=i^∂x∂+j^∂y∂+k^∂z∂
Used to define gradient, divergence, and curl.
Laplacian Operator
∇2f=∇⋅(∇f)=∂x2∂2f+∂y2∂2f+∂z2∂2f
Used in heat equation, wave equation, Poisson’s equation.
Important Vector Identities
∇⋅(∇×A)=0 ∇×(∇f)=0 ∇⋅(fA)=f(∇⋅A)+A⋅(∇f) ∇×(fA)=f(∇×A)+∇f×A
🔹 2️⃣ Vector Integration
Ordinary Integrals of Vectors
If A(t) is a vector-valued function:∫A(t)dt=(∫Axdt)i^+(∫Aydt)j^+(∫Azdt)k^
Multiple Integrals
Used to integrate over regions of:
- Line (1D)
- Surface (2D)
- Volume (3D)
Jacobian
For transformation from variables (x,y,z) to (u,v,w):J=∂(u,v,w)∂(x,y,z)=∂u∂x∂u∂y∂u∂z∂v∂x∂v∂y∂v∂z∂w∂x∂w∂y∂w∂z
Important in changing coordinates (cartesian → cylindrical → spherical).
🔹 Infinitesimal Elements
| Type | Symbol | Example |
|---|---|---|
| Line | dr | along a curve |
| Surface | dS | tiny patch of a surface |
| Volume | dV | tiny block in space |
🔹 Line Integral of a Vector Field
∫CA⋅dr
Used in work done by a force field.
🔹 Surface Integral
∬SA⋅dS
Measures flux crossing a surface.
🔹 Volume Integral
∭VfdV
Used in computing charge, mass, or density over a volume.
⭐ Vector Theorems (Applications Only)
(1) Gauss’ Divergence Theorem
Relates volume integral of divergence to flux through boundary surface:∭V(∇⋅A)dV=∬SA⋅dS
(2) Stokes’ Theorem
Relates surface integral of curl to line integral around boundary curve:∬S(∇×A)⋅dS=∮CA⋅dr
(3) Green’s Theorem (2D version of Stokes)
∮C(Pdx+Qdy)=∬R(∂x∂Q−∂y∂P)dA
Applications:
- Fluid flow
- Electromagnetic theory
- Heat and wave studies
📌 Conclusion
| Topic | Key Idea |
|---|---|
| Vector differentiation | Measures change (gradient/divergence/curl) |
| Vector integration | Measures accumulated effect in space |
| Theorems | Convert difficult integrals into simpler geometrical forms |
These concepts form the backbone of sciences and engineering, especially electromagnetism, fluid mechanics, robotics, and quantum physics.




